(Editor's Note: This article is presented in the form of a commented program. You can download the full source and check it out for a full primer! This article includes the fully code and comments, too)

Welcome back! In this installment I'm going to simply show you a way to have more then one "entity" on screen. To do this I'm just going to make some modifications [actualy a re-write :) ] of the previous example. Last time I showed you a basic example of rotation and translation that involved recreating the player's ship from ASTEROIDS. This time we are going to add some asteroids, and a variety of ways for the "player" to control what happens to them...

ASTEROIDS as a primer to 3d

 
To do this we are going to use 2 different 3D line models [or 3D objects that are constructed from lines rather than polygons]. The models will be in 3D, but we are still only going to rotate along the Z-axis. We are also going to use a very simple way to project the 3D points to the screen.

To begin, we are only going to use these three subs:

DECLARE SUB makemodels ()
DECLARE SUB drawframe ()
DECLARE SUB moveent ()

Sub makemodels initiates the data array fields to the begining values. Sub drawframe performs all the transforms, projection and drawing to the screen. Sub moveent performs all the "physics" on the entities.

We will also use these data types:

TYPE pntdat
x AS INTEGER
y AS INTEGER
END TYPE

Type pntdat is used by the entities to hold location and vector values we also used it last time in holding the "model" of the space ship.

TYPE ddddat
x AS INTEGER
y AS INTEGER
z AS INTEGER
END TYPE

Type ddddat [for "3D data"] is used to hold a 3D point. this is only used by the 3D line models to hold the endpoints of each 3D line.

TYPE lndat
v1 AS ddddat
v2 AS ddddat
c AS INTEGER
END TYPE

Type lndat [for "line data"] holds one 3D line. the "v1" and "v2" contain the endpoints while "c" contains the line color.

TYPE entdat
scale AS SINGLE
location AS pntdat
vector AS pntdat
angle AS INTEGER
turnspd AS INTEGER
thrust AS INTEGER
END TYPE

Type entdat [for "entity data"] contains all the information we will use for a single entity. "scale" [a floating point value] is used to "resize" the entity when transforming it's "object" [or model] to "world space" [a scale of < 1 but > 0 will make it smaller, while > 1 makes it larger] Location and vector hold the 2D [x and y] point used to describe where the entity is and where it is going. Angle indicates what direction the entity is faceing, and turnspd is used to make the entity turn. Thrust is used with the vector to get the entity moveing.

DIM SHARED obj(2, 12) AS lndat

Now then this array called obj [for "object"] is what will hold the 3D line models. The "2" indicates that we have two models and the "12" means that they each contain twelve 3D lines.

DIM SHARED ent(10) AS entdat

DIM SHARED player AS INTEGER

The ent array contains the entity values, and player is basicaly used as a "pointer" to the ent array. It indicated which entity the player is in control of [by doing this the "player" can control any one of the entities]

player = 1

But we will start by setting entity number 1 under the player's control

SCREEN 7, 0, 1, 0
WINDOW (-160, -100)-(160, 100)

You may remember this from last time. We are going to use SCREEN 7 for this simply because it allows us to have "flickerless" animation. The Window command is used to help convert "world space" to "camera space" [we won't use this once we get to performing real 3D...I promise:)]

makemodels

Okay we start by setting up all the models and getting are start-up values.

DO

Now we are in the "main-loop". The basic idea is to [step 1] draw a frame. Then [step 2] get the player's input from the keyboard. Finaly [step 3] perform the neccessary calculations to each entity [including anything special that the player indicated to do in step 2] Repeat back to step 1 until time to quit...

drawframe

Here we perform step 2:

SELECT CASE INKEY$

Player presses up...meaning thrust forward

CASE CHR$(0) + CHR$(72)
ent(player).thrust = -1

Press down...reverse thrust

CASE CHR$(0) + CHR$(80)
ent(player).thrust = 1

Turn left, then turn right

CASE CHR$(0) + CHR$(75)
ent(player).turnspd = -8

CASE CHR$(0) + CHR$(77)
ent(player).turnspd = 8

Player presses [SPACE BAR]...we stop the entities movement

CASE " "
ent(player).vector.x = 0
ent(player).vector.y = 0
ent(player).thrust = 0

Pressing this will shrink the model, the next will enlarge the model

CASE "-", "_"
ent(player).scale = ent(player).scale - .1
IF ent(player).scale < .01 THEN ent(player).scale = .1

CASE "+", "="
ent(player).scale = ent(player).scale + .1
IF ent(player).scale > 2 THEN ent(player).scale = 2

Ma Snart shows ya how to make this

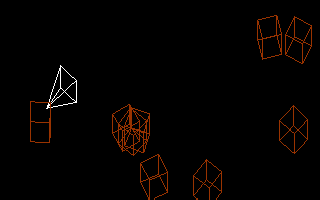
This will "toggle" player control to the next numericaly lower entity

CASE "[", "{"
player = player - 1
IF player < 1 THEN player = 10

And this will make the next numericaly higher entity fall under the player's control

CASE "]", "}"
player = player + 1
IF player > 10 THEN player = 1

The quit key...

CASE CHR$(27)
quit = 1
END SELECT

Then were on to step 3:

moveent
LOOP UNTIL quit = 1

All done....

END

In the program is the 3D line model data for both objects.. The player's "ship" is first, followed by the "asteroid" Each model has 12 3D lines; each DATA statement contains one line in this format:

' X1 , Y1 , Z1 , X2 , Y2 , Z2 , Color

Remeber each 3D point is in reference to the center [or zero] of "object space". In THIS program:

• a +X is to the right while a -X is to the left
• a +Y is to the bottom while a -Y is to the top
• a -Z is to the TOP and a +Z is to the bottom

'Player's "ship":
DATA -10,10,10,10,10,10,15
DATA -10,10,-10,10,10,-10,15
DATA -10,10,10,-10,10,-10,15
DATA 10,10,10,10,10,-10,15
DATA 10,10,10,0,-20,0,15
DATA 10,10,-10,0,-20,0,15
DATA -10,10,10,0,-20,0,15
DATA -10,10,-10,0,-20,0,15
DATA 0,0,0,0,0,0,0
DATA 0,0,0,0,0,0,0
DATA 0,0,0,0,0,0,0
DATA 0,0,0,0,0,0,0

'The "asteroid"
DATA -20,20,20,20,20,20,6
DATA -20,20,-20,20,20,-20,6
DATA -20,-20,20,20,-20,20,6
DATA -20,-20,-20,20,-20,-20,6
DATA -20,-20,-20,-20,20,-20,6
DATA -20,-20,20,-20,20,20,6
DATA 20,-20,-20,20,20,-20,6
DATA 20,-20,20,20,20,20,6
DATA -20,-20,-20,-20,-20,20,6
DATA -20,20,-20,-20,20,20,6
DATA 20,-20,-20,20,-20,20,6
DATA 20,20,-20,20,20,20,6
'end of data...

Ok. This is the first sub, drawframe. It will, as you probably supposed, draw the objects to the screen using SCREEN 7 stuff.

SUB drawframe

CLS

Start by clearing the frame

FOR i = 1 TO 10

Here we start a FOR/NEXT loop to transform the "object space" to the "world space" for each entity.

ex = ent(i).location.x
ey = ent(i).location.y
ea = ent(i).angle

Then put the entities values into temporary variables

sv! = SIN(ea * 3.141593 / 180)
cv! = COS(ea * 3.141593 / 180)

Because the entity is facing the one angle we can calculate the SIN and COS before we rotate each point of the model.

sc! = ent(i).scale

Put the entity scale value into a temp variable

IF i = player THEN
model = 1
ELSE
model = 2
END IF

This sets up which object we will transform based on the player value.

FOR j = 1 TO 12

We will now transform each line of the object to "world space"

dx1 = obj(model, j).v1.x * cv! + obj(model, j).v1.y * sv!
dy1 = obj(model, j).v1.y * cv! - obj(model, j).v1.x * sv!

dx2 = obj(model, j).v2.x * cv! + obj(model, j).v2.y * sv!
dy2 = obj(model, j).v2.y * cv! - obj(model, j).v2.x * sv!

First we rotate each end-point of the objects line

dx1 = (dx1 * sc!) + ex
dx2 = (dx2 * sc!) + ex
dy1 = ((dy1 + obj(model, j).v1.z) * sc!) + ey
dy2 = ((dy2 + obj(model, j).v2.z) * sc!) + ey

Then transform it by adding the vector created by the location of the entity in "world space". But before we did that we multipliyed the point by the entities scale value [this is what makes it different sizes]. And before doing that to the Y values we add the corisponding Z [this is what causes the 3/4 or isometric view to work, and could also be considered "projection"].

So a basic isometric "projection" formula would be:
projectedX = rotated_and_translated_X
projectedY = rotated_and_translated_Y + pointZ

LINE (dx1, dy1)-(dx2, dy2), obj(model, j).c

then we draw the line [remember our transformation of "world space" to "camera space" is being handled by the WINDOW statement earlyer]

NEXT j

NEXT i

PCOPY 1, 0

All done...so we show what we did :)

END SUB

This next sub draws out the models based on the DATA

SUB makemodels

RANDOMIZE TIMER

Here we are going to put the 3D line models together by reading the values in from the DATA statements.

FOR i = 1 TO 2
FOR j = 1 TO 12

READ obj(i, j).v1.x
READ obj(i, j).v1.y
READ obj(i, j).v1.z

READ obj(i, j).v2.x
READ obj(i, j).v2.y
READ obj(i, j).v2.z

READ obj(i, j).c

NEXT j
NEXT i

Now we set up the entities by picking random numbers for most of the fields.

FOR i = 1 TO 10

ent(i).scale = .5

I'll start by making each entity's object 1/2 size

ent(i).location.x = INT(RND * 320) - 160
ent(i).location.y = INT(RND * 200) - 100
ent(i).angle = INT(RND * 360)

And face them in a random direction at a random point

ent(i).turnspd = INT(RND * 16) - 8
ent(i).thrust = INT(RND * 6) - 4

And a random turning speed and thrust [remember a negative value means they are going forward]

NEXT i

END SUB

Almost done.

SUB moveent

Here we perform entity calculations. This is the segment of the engine where collision detection and other "physics" would be calculated on the entities.

FOR i = 1 TO 10

ent(i).location.x = ent(i).location.x + ent(i).vector.x
ent(i).location.y = ent(i).location.y + ent(i).vector.y

First we move each entity by the entities vector

ent(i).vector.x = ent(i).vector.x + (ent(i).thrust * SIN(ent(i).angle * 3.141593 / 180))
ent(i).vector.y = ent(i).vector.y + (ent(i).thrust * COS(ent(i).angle * 3.141593 / 180))

We then calculate the vector given the value of thrust. Notice the formula seems new, but it isn't Remember our Z-axis rotation formula from last time?
rotatedX = pointX * COS(angle) + pointY * SIN(angle)
rotatedY = pointY * COS(angle) - pointX * SIN(angle)
Well, in our little ASTEROIDS engine to move forward you decrease Y [or -Y] and to move backwards you increase Y [or +Y]...anything in X would mean we were moving sideways...What we are doing is rotating a vector [in this case thrust] to the orientation of the entity [measured by the angle]

In this case or thrust vector's X = 0...and anything mutiplyed by 0 = 0 So we can optimize the formula by removing the need to multiply 0 by the SIN and COS of the angle [the result would be 0 anyway].

So our thrust vecter formula is:
thrustX = thrust * SIN(angle)
thrustY = thrust * COS(angle)

ent(i).angle = ent(i).angle + ent(i).turnspd

Here we change the angle by the amount of turnspd [if turnspd = 0 the angle remains the same]

IF ent(i).location.x > 160 THEN ent(i).location.x = ent(i).location.x - 320
IF ent(i).location.x < -160 THEN ent(i).location.x = ent(i).location.x + 320
IF ent(i).location.y > 100 THEN ent(i).location.y = ent(i).location.y - 200
IF ent(i).location.y < -100 THEN ent(i).location.y = ent(i).location.y + 200

IF ent(i).angle > 360 THEN ent(i).angle = ent(i).angle - 360
IF ent(i).angle < 0 THEN ent(i).angle = ent(i).angle + 360

Here we are keeping our entity in the bounds of our "world space" and keeping the angle between 0 and 360.

IF ent(i).thrust > 0 THEN ent(i).thrust = ent(i).thrust - 1
IF ent(i).thrust < 0 THEN ent(i).thrust = ent(i).thrust + 1

Here we are returning thrust to 0. If thrust always stayed at some value other then 0 the entity would always be accelerateing [we don't want that!]

IF i = player THEN
IF ent(i).turnspd > 0 THEN ent(i).turnspd = ent(i).turnspd - 1
IF ent(i).turnspd < 0 THEN ent(i).turnspd = ent(i).turnspd + 1
END IF

Here if the entity is the same as the one pointed to by player. We are going to return turnspd to 0 [if 0 the entity isn't turning] this is done so that the player has control over where the entity is faceing [else the entity is constantly rotating if not equal to 0]

NEXT i

END SUB

That's all for this time. Run the program and have fun with it. Check back in April for more!

Find out why MA SNART doesn't cover the easy stuff like Bezier curves in this series by emailing him here.

Download the fully commented program!