By EvilGeek (e-mail withheld on request)
In this article, i'm only going to handle the 2d case of convex hull. The convex hull of a set of points is the smallest convex polygon containing all of the points. This is a helpful thing to know when creating isosurfaces, and a bunch of other shit.
Suppose we want to take the convex hull of the points in fig. 1 for a moment. How would we go about doing this? There are several algorithms for finding the convex hull, but I won't describe some of them. If you want more info, look at the bibliography at the end of this article. The slowest method (runs in n^4 time) is to test each point (n) against every single possible triangle in the data (n^3). If the point is interior to any of the triangles, we discard it (testing interiority by using the walk-north algorithm).
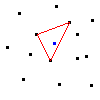
Needless to say, we don't have time for n^4 operations to find the convex hull of something (the convex hull of just 20 points would be 20^4 = 160000 tests), so nerds have developed more efficient algorithms. There's an n^3 algorithm which is very similar to the n^4 algorithm described above. If you want an n^3 algorithm too badly, look in the biblio. The gift-wrapping algorithm is the next one I will discuss here, and I believe it runs in n^2 time. Basically, the principle of this algorithm is that you take the lowest point, then you find the line with the lowest angle (closest to horizontal), repeat (except you find the closest to the last angle), until you end up at the first point again.
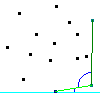
Wow, that's a significant improvement, from n^4 to n^2, but we can do better. We can use the quickhull algorithm, which takes the highest, lowest, leftmost, and rightmost points as a guess polygon, and checks each point to see if it is interior. If not, we add it to the convex hull. One thing that you can easily fuck up with this algorithm is testing to see if formerly exterior points are now interior, and if so, removing them.
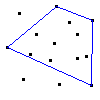
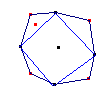
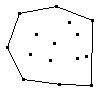
And here's our convex hull: