By Ethan Winer <ethan@ethanwiner.com>
In Chapter 1 you examined the role of a compiler, and learned how it translates BASIC source code into the assembly language commands a PC requires. But no matter how important the compiler is when creating a final executable program, it is only half of the story. This chapter discusses the equally important other half: data. Indeed, some form of data is integral to the operation of every useful program you will ever write. Even a program that merely prints "Hello" to the display screen requires the data "Hello".
Data comes in many shapes and sizes, starting with a single bit, continuing through eight-byte double precision variables, and extending all the way to multi-megabyte disk files. In this chapter you will learn about the many types of data that are available to you, and how they are manipulated in a BASIC program. You will also learn how data is stored and assigned, and how BASIC's memory management routines operate.
Compiled BASIC supports two fundamental types of data (numeric and string), two primary methods of storage (static and dynamic), and two kinds of memory allocation (near and far). Of course, the myriad of data types and methods is not present to confuse you. Rather, each is appropriate in certain situations. By fully understanding this complex subject, you will be able to write programs that operate as quickly as possible, and use the least amount of memory.
I will discuss each of the following types of data: integer and floating point numeric data, fixed-length and dynamic (variable-length) string data, and user-defined TYPE variables. Besides variables which are identified by name, BASIC supports named constant data such as literal numbers and quoted strings.
I will also present a complete comparison of the memory storage methods used by BASIC, to compare near versus far storage, and dynamic versus static allocation. It is important to understand that near storage refers to variables and other data that compete for the same 64K data space that is often referred to as Near Memory or Data Space. By contrast, far storage refers to the remaining memory in a PC, up to the 640K limit that DOS imposes.
The distinction between dynamic and static allocation is also important to establish now. Dynamic data is allocated in whatever memory is available when a program runs, and it may be resized or erased as necessary. Static data, on the other hand, is created by the compiler and placed directly into the .EXE file. Therefore, the memory that holds static data may not be relinquished for other uses.
Each type of data has its advantages and disadvantages, as does each storage method. To use an extreme example, you could store all numeric data in string variables if you really wanted to. But this would require using STR$ every time a value was to be assigned, and VAL whenever a calculation had to be made. Because STR$ and VAL are relatively slow, using strings this way will greatly reduce a program's performance. Further, storing numbers as ASCII digits can also be very wasteful of memory. That is, the double precision value 123456789.12345 requires fifteen bytes, as opposed to the usual eight.
Much of BASIC's broad appeal is that it lets you do pretty much anything you choose, using the style of programming you prefer. But as the example above illustrates, selecting an appropriate data type can have a decided impact on a program's efficiency. With that in mind, let's examine each kind of data that can be used with BASIC, beginning with integers.
An integer is the smallest unit of numeric storage that BASIC supports, and it occupies two bytes of memory, or one "word". Although various tricks can be used to store single bytes in a one-character string, the integer remains the most compact data type that can be directly manipulated as a numeric value. Since the 80x86 microprocessor can operate on integers directly, using them in calculations will be faster and require less code than any other type of data. An integer can hold any whole number within the range of -32768 to 32767 inclusive, and it should be used in all situations where that range is sufficient. Indeed, the emphasis on using integers whenever possible will be a recurring theme throughout this book.
When the range of integer values is not adequate in a given programming situation, a long integer should be used. Like the regular integer, long integers can accommodate whole numbers only. A long integer, however, occupies four bytes of memory, and can thus hold more information. This yields an allowable range of values that spans from -2147483648 through 2147483647 (approximately +/- 2.15 billion). Although the PC's processor cannot directly manipulate a long integer in most situations, calculations using them will still be much faster and require less code when compared to floating point numbers.
Regardless of which type of integer is being considered, the way they are stored in memory is very similar. That is, each integer is comprised of either two or four bytes, and each of those bytes contains eight bits. Since a bit can hold a value of either 0 or 1 only, you can see why a larger number of bits is needed to accommodate a wider range of values. Two bits are required to count up to three, three bits to count to seven, four bits to count to fifteen, and so forth.
A single byte can hold any value between 0 and 255, however that same range can also be considered as spanning from -128 to 127. Similarly, an integer value can hold numbers that range from either 0 to 65535 or -32768 through 32767, depending on your perspective. When the range is considered to be 0 to 65535 the values are referred to as unsigned, because only positive values may be represented. BASIC does not, however, support unsigned integer values. Therefore, that same range is used in BASIC programs to represent values between -32768 and 32767. When integer numbers are considered as using this range they are called signed.
If you compile and run the short program in the listing that follows, the transition from positive to negative numbers will show how BASIC treats values that exceed the integer range of 32767. Be sure not to use the /d debugging option, since that will cause an overflow error to be generated at the transition point. The BASIC environment performs the same checking as /d does, and it too will report an error before this program can run to completion.
Number% = 32760
FOR X% = 1 TO 14
Number% = Number% + 1
PRINT Number%,
NEXT
Displayed result:
32761 32762 32763 32764 32765 32766 32767 -32768 -32767 -32766 -32765 -32764 -32763 -32762 -32761
As you can see, once an integer reaches 32767, adding 1 again causes the value to "wrap" around to -32768. When Number% is further incremented its value continues to rise as expected, but in this case by becoming "less negative". In order to appreciate why this happens you must understand how an integer is constructed from individual bits. I am not going to belabor binary number theory or other esoteric material, and the brief discussion that follows is presented solely in the interest of completeness.
Sixteen bits are required to store an integer value. These bits are numbered 0 through 15, and the least significant bit is bit number 0. To help understand this terminology, consider the decimal number 1234. Here, 4 is the least significant digit, because it contributes the least value to the entire number. Similarly, 1 is the most significant portion, because it tells how many thousands there are, thus contributing the most to the total value. The binary numbers that a PC uses are structured in an identical manner. But instead of ones, tens, and hundreds, each binary digit represents the number of ones, twos, fours, eights, and so forth that comprise a given byte or word.
To represent the range of values between 0 and 32767 requires fifteen bits, as does the range from -32768 to -1. When considered as signed numbers, the most significant bit is used to indicate which range is being considered. This bit is therefore called the sign bit. Long integers use the same method except that four bytes are used, so the sign bit is kept in the highest position of the fourth byte.
Selected portions of the successive range from 0 through -1 (or 65535) are shown in Table 2-1, to illustrate how binary counting operates. When counting with decimal numbers, once you reach 9 the number is wrapped around to 0, and then a 1 is placed in the next column. Since binary bits can count only to one, they wrap around much more frequently. The Hexadecimal equivalents are also shown in the table, since they too are related to binary numbering. That is, any Hex value whose most significant digit is 8 or higher is by definition negative.
| Signed | Unsigned | ||
| Decimal | Decimal | Binary | Hex |
| 0 | 0 | 0000 0000 0000 0000 | 0000 |
| 1 | 1 | 0000 0000 0000 0001 | 0001 |
| 2 | 2 | 0000 0000 0000 0010 | 0002 |
| 3 | 3 | 0000 0000 0000 0011 | 0003 |
| 4 | 4 | 0000 0000 0000 0100 | 0004 |
| . | . | . | . |
| . | . | . | . |
| 32765 | 32765 | 0111 1111 1111 1101 | 7FFD |
| 32766 | 32767 | 0111 1111 1111 1110 | 7FFE |
| 32767 | 32767 | 0111 1111 1111 1111 | 7FFF |
| -32768 | 32768 | 1000 0000 0000 0000 | 8000 |
| -32767 | 32769 | 1000 0000 0000 0001 | 8001 |
| -32766 | 32770 | 1000 0000 0000 0010 | 8002 |
| . | . | . | . |
| . | . | . | . |
| -4 | 65531 | 1111 1111 1111 1100 | FFFB |
| -3 | 65532 | 1111 1111 1111 1101 | FFFC |
| -2 | 65533 | 1111 1111 1111 1110 | FFFD |
| -1 | 65534 | 1111 1111 1111 1111 | FFFE |
| 0 | 65535 | 0000 0000 0000 0000 | FFFF |
Before we can discuss such issues as variable and data storage, a few terms must be clarified. A memory address is a numbered location in which a given piece of data is said to reside. Addresses refer to places that exist in a PC's memory, and they are referenced by those numbers. Every PC has thousands of memory addresses in which both data and code instructions may be stored.
A pointer is simply a variable that holds an address. Consider a single precision variable named Value that has been stored by the compiler at memory address 10. If another variable--let's call it Address%--is then assigned the value 10, Address% could be considered to be a pointer to Value. Pointer variables are the bread and butter of languages such as C and assembler, because data is often read and written by referring to one variable which in turn holds the address of another variable.
Although BASIC shields you as the programmer from such details, pointers are in fact used internally by the BASIC language library routines. This method of using pointers is sometimes called indirection, because an additional, indirect step is needed to first go to one variable, get an address, and then go to that address to access the actual data. Now let's see how these memory issues affect a BASIC program.
When a conventional two-byte integer is stored in the PC's memory, the lower byte is kept in the lower memory address. For example, if X% is said to reside at address 10, then the least significant byte is at address 10 and the most significant byte is at address 11. Likewise, a long integer stored at address 102 actually occupies addresses 102 through 105, with the least significant portion at the lowest address. This is shown graphically in Figure 2-1.
Figure 2-1: An integer is stored in two adjacent memory locations, with the Least Significant Byte at the lower address, and the Most Significant Byte at the higher. |
This arrangement certainly seems sensible, and it is. However, some people get confused when looking at a range of memory addresses being displayed, because the values in lower addresses are listed at the left and the higher address values are shown on the right. For example, the DEBUG utility that comes with DOS will display the Hex number ABCD as CD followed by AB. I mention this only because the order in which digits are displayed will become important when we discuss advanced debugging in Chapter 4.
In case you are wondering, the compiler assigns addresses in the order in which variables are encountered. The first address used is generally 36 Hex, so in the program below the variables will be stored at addresses 36, 38, 3A, and then 3C. Hex numbering is used for these examples because that's the way DEBUG and CodeView report them.
A% = 1 'this is at address &H36 B% = 2 'this is at address &H38 C% = 3 'this is at address &H3A D% = 4 'this is at address &H3C
Floating point variables and numbers are constructed in an entirely different manner than integers. Where integers and long integers simply use the entire two or four bytes to hold a single binary number, floating point data is divided into portions. The first portion is called the mantissa, and it holds the base value of the number. The second portion is the exponent, and it indicates to what power the mantissa must be raised to express the complete value. Like integers, a sign bit is used to show if the number is positive or negative.
The structure of single precision values in both IEEE and the original proprietary Microsoft Binary Format (MBF) is shown in Figure 2-2. For IEEE numbers, the sign bit is in the most significant position, followed by eight exponent bits, which are in turn followed by 23 bits for the mantissa. Double precision IEEE values are structured similarly, except eleven bits are used for the exponent and 52 for the mantissa.
Double precision MBF numbers use only eight bits for an exponent rather than eleven, trading a reduced absolute range for increased resolution. That is, there are fewer exponent bits than the IEEE method uses, which means that extremely large and extremely small numbers cannot be represented. However, the additional mantissa bits offer more absolute digits of precision.
The IEEE format:
| SEEEEEEE | EMMMMMMM | MMMMMMMM | MMMMMMMM |
The MBF format:
| EEEEEEEE | SMMMMMMM | MMMMMMMM | MMMMMMMM |
Notice that with IEEE numbers, the exponent spans a byte boundary. This undoubtedly contributes to the slow speed that results from using numbers in this format when a coprocessor is not present. Contrast that with Microsoft's MBF format in which the sign bit is placed between the exponent and mantissa. This allows direct access to the exponent with fewer assembler instructions, since the various bits don't have to be shifted around.
The IEEE format is used in QuickBASIC 4.0 and later, and BASIC PDS unless the /fpa option is used. BASIC PDS uses the /fpa switch to specify an alternate math package which provides increased speed but with a slightly reduced accuracy. Although the /fpa format is in fact newer than the original MBF used in interpreted BASIC and QuickBASIC 2 and 3, it is not quite as fast.
As was already mentioned, double precision data requires twice as many bytes as single precision. Further, due to the inherent complexity of the way floating point data is stored, an enormous amount of assembly language code is required to manipulate it. Common sense therefore indicates that you would use single precision variables whenever possible, and reserve double precision only for those cases where the added accuracy is truly necessary. Using either floating point variable type, however, is still very much slower than using integers and long integers. Worse, rounding errors are inevitable with any floating point method, as the following short program fragment illustrates.
FOR X% = 1 TO 10000
Number! = Number! + 1.1
NEXT
PRINT Number!
Displayed result:
10999.52
Although the correct answer should be 11000, the result of adding 1.1 ten thousand times is incorrect by a small amount. If you are writing a program that computes, say, tax returns, even this small error will be unacceptable. Recognizing this problem, Microsoft developed a new Currency data type which was introduced with BASIC PDS version 7.0.
The Currency data type is a cross between an integer and a floating point number. Like a double precision value, Currency data also uses eight bytes for storage. However, the numbers are stored in an integer format with an implied scaling of 10000. That is, a binary value of 1 is used to represent the value .0001, and a binary value of 20000 is treated as a 2. This yields an absolute accuracy to four decimal places, which is more than sufficient for financial work. The absolute range of Currency data is plus or minus 9.22 times 10 ^ 14 (ρ 9.22E14 or 922,000,000,000,000.0000), which is very wide indeed. This type of storage is called Fixed-Point, because the number of decimal places is fixed (in this case at four places).
Currency data offers the best compromise of all, since only whole numbers are represented and the fractional portion is implied. Further, since a separate exponent and mantissa are not used, calculations involving Currency data are extremely fast. In practice, a loop that adds a series of Currency variables will run about half as fast as the same loop using long integers. Since twice as many bytes must be manipulated, the net effect is an overall efficiency that is comparable to long integers. Compare that to double precision calculations, where manipulating the same eight bytes takes more than six times longer.
As you have seen, there is a great deal more to "simple" numeric data than would appear initially. But this hardly begins to scratch the surface of data storage and manipulation in BASIC. We will continue our tour of BASIC's data types with conventional dynamic (variable-length) strings, before proceeding to fixed-length strings and TYPE variables.
One of the most important advantages that BASIC holds over all of the other popular high-level languages is its support for dynamic string data. In Pascal, for example, you must declare every string that your program will use, as well as its length, before the program can be compiled. If you determine during execution of the program that additional characters must be stored in a string, you're out of luck.
Likewise, strings in C are treated internally as an array of single character bytes, and there is no graceful way to extend or shorten them. Specifying more characters than necessary will of course waste memory, and specifying too few will cause subsequent data to be overwritten. Since C performs virtually no error checking during program execution, assigning to a string that is not long enough will corrupt memory. And indeed, problems such as this cause untold grief for C programmers.
Dynamic string memory handling is built into BASIC, and those routines are written in assembly language. BASIC is therefore extremely efficient and very fast in this regard. Since C is a high-level language, writing an equivalent memory manager in C would be quite slow and bulky by comparison. I feel it is important to point out BASIC's superiority over C in this regard, because C has an undeserved reputation for being a very fast and powerful language.
Compiled BASIC implements dynamic strings with varying lengths by maintaining a string descriptor for each string. A string descriptor is simply a four-byte table that holds the current length of the string as well as its current address. The format for a BASIC string descriptor is shown in Figure 2-3. In QuickBASIC programs and BASIC PDS when far strings are not specified, all strings are stored in an area of memory called the near heap. The string data in this memory area is frequently shuffled around, as new strings are assigned and old ones are abandoned.
| Higher Addresses ^ | | | | | ||||
| <-- Address | |||
| <-- Length | <----- VARPTR(Work$) |
The lower two bytes in a string descriptor together hold the current length of the string, and the second two bytes hold its address. The memory location at the bottom of Figure 2-3 is at the lowest address. The short program below shows how you could access a string by peeking at its descriptor.
DEFINT A-Z Test$ = "BASIC Techniques and Utilities" Descr = VARPTR(Test$) Length = PEEK(Descr) + 256 * PEEK(Descr + 1) Addr = PEEK(Descr + 2) + 256 * PEEK(Descr + 3) PRINT "The length is"; Length PRINT "The address is"; Addr PRINT "The string contains "; FOR X = Addr TO Addr + Length - 1 PRINT CHR$(PEEK(X)); NEXT
Displayed result:
The length is 17 The address is 15646 (this will vary) The string contains BASIC Techniques and Utilities
Each time a string is assigned or reassigned, memory in the heap is claimed and the string's descriptor is updated to reflect its new length and address. The old data is then marked as being abandoned, so the space it occupied may be reclaimed later on if it is needed. Since each assignment claims new memory, at some point the heap will become full. When this happens, BASIC shuffles all of the string data that is currently in use downward on top of the older, abandoned data. This heap compaction process is often referred to colorfully as *garbage collection*.
In practice, there are two ways to avoid having BASIC claim new space for each string assignment--which takes time--and you should consider these when speed is paramount. One method is to use LSET or RSET, to insert new characters into an existing string. Although this cannot be used to make a string longer or shorter, it is very much faster than a straight assignment which invokes the memory management routines. The second method is to use the statement form of MID$, which is not quite as fast as LSET, but is more flexible.
Microsoft BASIC performs some additional trickery as it manages the string data in a program. For example, whenever a string is assigned, an even number of bytes is always requested. Thus, if a five-character string is reassigned to one with six characters, the same space can be reused. Since claiming new memory requires a finite amount of time and also causes garbage collection periodically, this technique helps to speed up the string assignment process.
For example, in a program that builds a string by adding new characters to the end in a loop, BASIC can reduce the number of times it must claim new memory to only every other assignment. Another advantage to always allocating an even number of bytes is that the 80286 and later microprocessors can copy two-byte words much faster than they can copy the equivalent number of bytes. This has an obvious advantage when long strings are being assigned.
In most cases, BASIC's use of string descriptors is much more efficient than the method used by C and other languages. In C, each string has an extra trailing CHR$(0) byte just to mark where it ends. While using a single byte is less wasteful than requiring a four-byte table, BASIC's method is many times faster. In C the entire string must be searched just to see how long it is, which takes time. Likewise, comparing and concatenating strings in C requires scanning both strings for the terminating zero character. The same operations in BASIC require but a single step to obtain the current length.
Pascal uses a method that is similar to BASIC's, in that it remembers the current length of the string. The length is stored with the actual string data, in a byte just before the first character. Unfortunately, using a single byte limits the maximum length of a Pascal string to only 255 characters. And again, when a string is shortened in Pascal, the extra characters are not released for use by other data. But it is only fair to point out that Pascal's method is both fast and compact. And since strings in C and Pascal never move around in memory, garbage collection is not required.
Although a BASIC string descriptor uses four bytes of additional memory beyond that needed for the actual data, this is only part of the story. An additional two bytes are needed to hold a special "variable" called a *back pointer*. A back pointer is an integer word that is stored in memory immediately before the actual string data, and it holds the address of the data's string descriptor. Thus, it is called a back pointer because it points back to the descriptor, as opposed to the descriptor which points to the data.
Because of this back pointer, six additional bytes are actually needed to store each string, beyond the number of characters that it contains. For example, the statement Work$ = "BASIC" requires twelve bytes of data memory--five for the string itself, one more because an even number of bytes is always claimed, four for the descriptor, and two more for a back pointer. Every string that is defined in a program has a corresponding descriptor which is always present, however a back pointer is maintained only while the string has characters assigned to it. Therefore, when a string is erased the two bytes for its back pointer are also relinquished.
I won't belabor this discussion of back pointers further, because understanding them is of little practical use. Suffice it to say that a back pointer helps speed up the heap compaction process. Since the address portion of the descriptor must be updated whenever the string data is moved, this pointer provides a fast link between the data being moved and its descriptor. By the way, the term "pointer" refers to any variable that holds a memory address, regardless of what language is being considered.
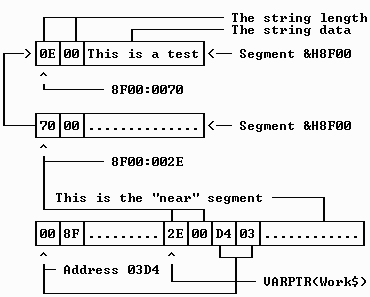
BASIC PDS offers an option to specify "far strings", whereby the string data is not stored in the same 64K memory area that holds most of a program's data. The method of storage used for far strings is of necessity much more complex than near strings, because both an address and a segment must be kept track of. Although Microsoft has made it clear that the structure of far string descriptors may change in the future, I would be remiss if this undocumented information were not revealed here. The following description is valid as of BASIC 7.1 [it is still valid for VB/DOS too].
For each far string in a program, a four-byte descriptor is maintained in near memory. The lower two bytes of the descriptor together hold the address of an integer variable that holds yet another address: that of the string length and data. The second pair of bytes also holds the address of a pointer, in this case a pointer to a variable that indicates the segment in which the string data resides. Thus, by retrieving the address and segment from the descriptor, you can locate the string's length and data, albeit with an extra level of indirection.
It is interesting to note that when far strings are being used, the string's length is kept just before its data, much like the way Pascal operates. Therefore, the address pointer holds the address of the length word which immediately precedes the actual string data.
The short program that follows shows how to locate all of the components of a far string based on examining its descriptor and related pointers. Notice that long integers are used to avoid the possibility of an overflow error if the segment or addresses happen to be higher than 32767. This way you can run the program in the QBX [or VB/DOS] editing environment. Figure 2-4 in turn illustrates the relationship between the address and pointer information graphically.
DEF FNPeekWord& (A&) FNPeekWord& = PEEK(A&) + 256& * PEEK(A& + 1) END DEF Work$ = "This is a test" DescAddr& = VARPTR(Work$) AddressPtr& = FNPeekWord&(DescAddr&) SegmentPtr& = FNPeekWord&(DescAddr& + 2) Segment& = FNPeekWord&(SegmentPtr&) DEF SEG = Segment& DataAddr& = FNPeekWord&(AddressPtr&) Length% = FNPeekWord&(DataAddr&) StrAddr& = DataAddr& + 2 PRINT "The descriptor address is:"; DescAddr& PRINT " The data segment is:"; Segment& PRINT " The length is:"; Length% PRINT "The string data starts at:"; StrAddr& PRINT " And the string data is: "; FOR X& = StrAddr& TO StrAddr& + Length% - 1 PRINT CHR$(PEEK(X&)); NEXT
Displayed result: (the addresses may vary)
The descriptor address is: 17220
The data segment is: 40787
The length is: 14
The string data starts at: 106
And the string data is: This is a test
Because two bytes are used to hold the segment, address, and length values, we must PEEK both of them and combine the results. This is the purpose of the PeekWord function that is defined at the start of the program. Note the placement of an ampersand after the number 256, which ensures that the multiplication will not cause an overflow error. I will discuss such use of numeric constants and type identifiers later in this chapter.

Even in a far-string program, some of the string data will be near. For example, DATA items and quoted string constants are stored in the same 64K DGROUP data segment that holds simple numeric and TYPE variables. The same "indirect" method is used, whereby you must look in one place to get the address of another address. In this case, however, the "far" segment that is reported is simply the normal near data segment. [DATA items in VB/DOS programs are still kept in near memory, but quoted strings are now kept in a separate segment.]
One final complication worth mentioning is that strings within a FIELD buffer (and possibly in other special situations) are handled slightly differently. Since all of the strings in a FIELD buffer must be contiguous, BASIC cannot store the length word adjacent to the string data. Therefore, a different method must be used. This case is indicated by setting the sign bit (the highest bit) in the length word as a flag. Since no string can have a negative length, that bit can safely be used for this purpose. When a string is stored using this alternate method, the bytes that follow the length word are used as additional pointers to the string's actual data segment and address.
One of the most important new features Microsoft added beginning with QuickBASIC 4.0 was fixed-length string and TYPE variables. Although fixed- length strings are less flexible than conventional BASIC strings, they offer many advantages in certain programming situations. One advantage is that they are static, which means their data does not move around in memory as with conventional strings. You can therefore obtain the address of a fixed-length string just once using VARPTR, confident that this address will never change. With dynamic strings, SADD must be used each time the address is needed, which takes time and adds code. Another important feature is that arrays of fixed-length strings can be stored in far memory, outside of the normal 64K data area. We will discuss near and far array memory allocation momentarily.
With every advantage, however, comes a disadvantage. The most severe limitation is that when a fixed-length string is used where a conventional string is expected, BASIC must generate code to create a temporary dynamic string, and then copy the data to it. That is, all of BASIC's internal routines that operate on strings expect a string descriptor. Therefore, when you print a fixed-length string, or use MID$ or INSTR or indeed nearly any statement or function that accepts a string, it must be copied to a form that BASIC's internal routines can accept. In many cases, additional code is created to delete the temporary string afterward. In others, the data remains until the next time the same BASIC statement is executed, and a new temporary string is assigned freeing the older one.
To illustrate, twenty bytes of assembly language code are required to print a fixed-length string, compared to only nine for a conventional dynamic string. Worse, when a fixed-length string is passed as an argument to a subprogram or function, BASIC not only makes a copy before passing the string, but it also copies the data back again in case the subroutine changed it! The extra steps the compiler performs are shown as BASIC equivalents in the listing that follows.
'----- This is the code you write: DIM Work AS STRING * 20 CALL TestSub(Work$) '----- This is what BASIC actually does: Temp$ = SPACE$(20) 'create a temporary string LSET Temp$ = Work$ 'copy Work$ to it CALL TestSub(Temp$) 'call the subprogram LSET Work$ = Temp$ 'copy the data back again Temp$ = "" 'erase the temporary data
As you can imagine, all of this copying creates an enormous amount of additional code in your programs. Where only nine bytes are required to pass a conventional string to a subprogram, 64 are needed when a fixed- length string is being sent. But you cannot assume unequivocally that conventional strings are always better or that fixed-length strings are always better. Rather, I can only present the facts, and let you decide based on the knowledge of what is really happening. In the discussion of debugging later in Chapter 4, you will learn how to use CodeView to see the code that BASIC generates. You can thus explore these issues further, and draw your own conclusions.
As I mentioned earlier, the TYPE variable is an important and powerful addition to modern compiled BASIC. Its primary purpose is to let programmers create composite data structures using any combination of native data types. C and Pascal have had such user-defined data types since their inception, and they are called Structures and Records respectively in each language.
One immediately obvious use for being able to create a new, composite data type is to define the structure of a random access data file. Another is to simulate an array comprised of varied types of data. Obviously, no language can support a mix of different data types within a single array. That is, an array cannot be created where some of the elements are, say, integer while others are double precision. But a TYPE variable lets you do something very close to that, and you can even create arrays of TYPE variables.
In the listing that follows a TYPE is defined using a mix of integer, single precision, double precision, and fixed-length string components. Also shown below is how a TYPE variable is dimensioned, and how each of its components are assigned and referenced.
TYPE MyType I AS INTEGER S AS SINGLE D AS DOUBLE F AS STRING * 20 END TYPE DIM MyData as MyType MyData.I = 12 'assign the integer portion MyData.S = 100.09 'and then the single part MyData.D = 43.2E56 'and then the double MyData.F = "Test" 'and finally the string PRINT MyData.F 'now print the string
Once the TYPE structure has been established, the DIM statement must be used to create an actual variable using that arrangement. Although DIM is usually associated with the definition of arrays, it is also used to identify a variable name with a particular type of data. In this case, DIM tells BASIC to set aside an area of memory to hold that many bytes. You may also use DIM with conventional variable types. For example, DIM LastName AS STRING or DIM PayPeriod AS DOUBLE lets you omit the dollar sign and pound sign when you reference them later in the program. In my opinion, however, that style leads to programs that are difficult to maintain, since many pages later in the source listing you may not remember what type of data is actually being referred to.
As you can see, a period is needed to indicate which portion of the TYPE variable is being referenced. The base name is that given when you dimensioned the variable, but the portion being referenced is identified using the name within the original TYPE definition. You cannot print a TYPE variable directly, but must instead print each component separately. Likewise, assignments to a TYPE variable must also be made through its individual components, with two exceptions. You may assign an entire TYPE variable from another identical TYPE directly, or from a dissimilar TYPE variable using LSET.
For example, if we had used DIM MyData AS MyType and then DIM HisData AS MyType, the entire contents of HisData could be assigned to MyData using the statement MyData = HisData. Had HisData been dimensioned using a different TYPE definition, then LSET would be required. That is, LSET MyData = HisData will copy as many characters from HisData as will fit into MyData, and then pad the remainder, if any, with blanks. It is important to understand that this behavior can cause strange results indeed. Since CHR$(32) blanks are used to pad what remains in the TYPE variable being assigned, numeric components may receive some unusual values. Therefore, you should assign differing TYPE variables only when those overlapping portions being assigned are structured identically.
With the introduction of BASIC PDS, programmers may also establish static arrays within a single TYPE definition. An array is dimensioned within a TYPE as shown in the listing that follows. As with a conventional DIM statement for an array, the number of elements are indicated and a non-zero lower bound may optionally be specified. Please understand, though, that you cannot use a variable for the number of elements in the array. That is, using PayHistory(1 TO NumDates) would be illegal.
TYPE ArrayType AmountDue AS SINGLE PayHistory(1 TO 52) AS SINGLE LastName AS STRING * 15 END TYPE DIM TypeArray AS ArrayType
There are several advantages to using an array within a TYPE variable. One is that you can reference a portion of the TYPE by using a variable to specify the element number. For example, TypeArray.PayHistory(PayPeriod) = 344.95 will assign the value 344.95 to element number PayPeriod. Without the ability to use an array, each of the 52 components would need to be identified by name. Further, arrays allows you to define a large number of TYPE elements with a single program statement. This can help to improve a program's readability.
Preceding sections have touched only briefly on the concept of static and dynamic memory storage. Let's now explore this subject in depth, and learn which methods are most appropriate in which situations.
By definition, static data is that which never changes in size, and never moves around in memory. In compiled BASIC this definition is further extended to mean all data that is stored in the 64K near memory area known as DGROUP. This includes all numeric variables, fixed-length strings, and TYPE variables. Technically speaking, the string descriptors that accompany each conventional (not fixed-length) string are also considered to be static, even though the string data itself is not. The string descriptors that comprise a dynamic string array, however, are dynamic data, because they move around in memory (as a group) and may be resized and erased.
Numeric arrays that are dimensioned with constant (not variable) subscripts are also static, unless the '$DYNAMIC metacommand has been used in a preceding program statement. That is, DIM Array#(0 TO 100) will create a static array, while DIM Array#(0 TO MaxElements) creates a dynamic array. Likewise, arrays of fixed-length strings and TYPE variables will be static, as long as numbers are used to specify the size.
There are advantages and disadvantages to each storage method. Access to static data is always faster than access to dynamic data, because the compiler knows the address where the data resides at the time it creates your program. It can therefore create assembly language instructions that go directly to that address. In contrast, dynamic data always requires a pointer to hold the current address of the data. An extra step is therefore needed to first get the data address from that pointer, before access to the actual data is possible. Static data is also in the near data segment, thus avoiding the need for additional code that switches segments.
The overwhelming disadvantage of static data, though, is that it may never be erased. Once a static variable or array has been used in a program, the memory it occupies can never be released for other uses. Again, it is impossible to state that static arrays are always better than dynamic arrays or vice versa. Which you use must be dictated by your program's memory requirements, when compared to its execution speed.
You have already seen how dynamic strings operate, by using a four-byte pointer table called a string descriptor. Similarly, a dynamic array also needs a table to show where the array data is located, how many elements there are, the length of each element, and so forth. This table is called an array descriptor, and it is structured as shown in Table 2-2.
There is little reason to use the information in an array descriptor in a BASIC program, and indeed, BASIC provides no direct way to access it anyway. But when writing routines in assembly language for use with BASIC, this knowledge can be quite helpful. As with BASIC PDS far string descriptors, none of this information is documented, and relying on it is most certainly not endorsed by Microsoft. Perhaps that's what makes it so much fun to discuss!
Technically speaking, only dynamic arrays require an array descriptor, since static arrays do not move or change size. But BASIC creates an array descriptor for every array, so only one method of code generation is necessary. For example, when you pass an entire array to a subprogram using empty parentheses, it is the address of the array descriptor that is actually sent. The subprogram can then access the data through that descriptor, regardless of whether the array is static or dynamic.
| Offset | Size | Description |
|---|---|---|
| 00 | 02 | Address where array data begins |
| 00 | 02 | Segment where that address resides |
| 04 | 02 | Far heap descriptor, pointer |
| 06 | 02 | Far heap descriptor, block size |
| 08 | 01 | Number of dimensions in the array |
| 09 | 01 | Array type and storage method: Bit 0 set = far array Bit 1 set = huge (/ah) array Bit 6 set = static array Bit 7 set = string array |
| 0A | 02 | Adjusted Offset |
| 0C | 02 | Length in bytes of each element |
| 0E | 02 | Number of elements in the last dimension (UBOUND - LBOUND + 1) |
| 10 | 02 | First element number in that dimension (LBOUND) |
| 12 | 02 | Number of elements in the second from last dimension |
| 14 | 02 | First element number in that dimension |
| . | 02 | Repeat number of elements and first element number as necessary, |
| . | 02 | through the first dimension |
The first four bytes together hold the segmented address where the array data proper begins in memory. Following the standard convention, the address is stored in the lower word, with the segment immediately following.
The next two words comprise the Far Heap Descriptor, which holds a pointer to the next dynamic array descriptor and the current size of the array. For static arrays both of these entries are zero. When multiple dynamic arrays are used in a program, the array descriptors are created in static DGROUP memory in the order BC encounters them. The Far Heap Pointer in the first array therefore points to the next array descriptor in memory. The last descriptor in the chain can be identified because it points to a word that holds a value of zero.
The block size portion of the Far Heap Descriptor holds the size of the array, using a byte count for string arrays and a "paragraph" count for numeric, fixed-length, and TYPE arrays. For string arrays--whether near or far--the byte count is based on the four bytes that each descriptor occupies. With numeric arrays the size is instead the number of 16-byte paragraphs that are needed to store the array.
The next entry is a single byte that holds the number of dimensions in the array. That is, DIM Array(1 TO 10) has one dimension and DIM Array(1 TO 10, 2 TO 20) has two.
The next item is also a byte, and it is called the Feature byte because the various bits it holds tell what type of array it is. As shown in the table, separate bits are used to indicate if the array is stored in far memory, whether or not /ah was used to specify huge arrays, if the array is static, and if it is a string array. Multiple bits are used for each of these array properties, since they may be active in combination. However, BASIC never sets the far and huge bits for string arrays, even when the PDS /fs option is used and the strings are in fact in far memory.
Of particular interest is the Adjusted Offset entry. Even though the segmented address where the array data begins is the first entry in the descriptor, it is useful only when the first element number in the array is zero. This would be the case with DIM Array(0 TO N), or simply DIM Array(N). To achieve the fastest performance possible when retrieving or assigning a given element, the Adjusted Offset is calculated when the array is dimensioned to compensate for an LBOUND other than 0.
For example, if an integer array is dimensioned starting at element 1, the Adjusted Offset is set to point two bytes before the actual starting address of the data. This way, the compiler can take the specified element number, multiply that times two (each element comprises two bytes), and then add that to the Adjusted Offset to immediately point at the correct element in memory. Otherwise, additional code would be needed to subtract the LBOUND value each time the array is accessed. Since the array's LBOUND is simply constant information, it would be wasteful to calculate that repeatedly at run time. Of course, the Adjusted Offset calculation is correspondingly more complex when dealing with multi-dimensional arrays.
The remaining entries identify the length of each element in bytes, and the upper and lower bounds. String arrays always have a 4 in the length location, because that's the length of each string descriptor. A separate pair of words is needed for each array subscript, to identify the LBOUND value and the number of elements. The UBOUND is not actually stored in the array descriptor, since it can be calculated very easily when needed. Notice that for multi-dimensional arrays, the last (right-most) subscript is identified first, followed by the second from the last, and continuing to the first one.
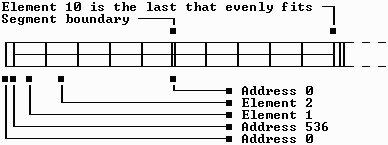
One final note worth mentioning about dynamic array storage is the location in memory of the first array element. For numeric arrays, the starting address is always zero, within the specified segment. (A new segment can start at any 16-byte address boundary, so at most 15 bytes may be wasted.) However, BASIC sometimes positions fixed-length string and TYPE arrays farther into the segment. BASIC will not allow an array element to span a segment boundary under any circumstances. This could never happen with numeric data, because each element has a length that is a power of 2. That is, 16,384 long integer elements will exactly fit in a single 64K segment. But when a fixed-length string or TYPE array is created, nearly any element length may be specified.
For example, if you use REDIM Array(1 TO 10) AS STRING * 13000, 130,000 bytes are needed and element 6 would straddle a segment. To prevent that from happening, BASIC's dynamic DIM routine fudges the first element to instead be placed at address 536. Thus, the last byte in element 5 will be at the end of the 64K segment, and the first byte in element 6 will fall exactly at the start of the second 64K code segment. The only limitation is that arrays with odd lengths like this can never exceed 128K in total size, because the inevitable split would occur at the start of the third segment. Arrays whose element lengths are a power of 2, such as 32 or 4096 bytes, do not have this problem. (Bear in mind that 1K is actually 1,024 bytes, so 128K really equals 131,072 bytes). This is shown graphically below in Figure 2-5.
You have already used the terms "near" and "far" to describe BASIC's data, and now let's see exactly what they mean. The 8086 family of microprocessors that are used in IBM PC and compatible computers use what is called a *segmented architecture*. This means that while an 8086 can access a megabyte of memory, it can do so only in 64K blocks at a time. Before you think this is a terrible way to design a CPU, consider the alternative.
For example, the 68000 family used in the Apple Macintosh and Atari computers use linear addressing, whereby any data anywhere may be accessed without restriction. But the problem is that with millions of possible addresses, many bytes are needed to specify those addresses. Because the data segment is implied when dealing with an 80x86, a single integer can refer to any address quickly and with very little code. Therefore, assembler instructions for the 68000 that reference memory tend to be long, making those programs larger.
Since being able to manipulate only one 64K segment is restrictive, the 8086's designers provided four different segment registers. One of these, the DS (Data Segment) register, is set to specify a single segment, which is then used by the program as much as possible. This data segment is also named DGROUP, and it holds all of the static data in a BASIC program. Again, data in DGROUP can be accessed much faster and with less code than can data in any other segment. In order to assign an element in a far array, for example, BASIC requires two additional steps which generates additional code. The first step is to retrieve the array's segment from the array descriptor, and the second is to assign the ES (Extra Segment) register to access the data.
Far data in a BASIC program therefore refers to any data that is outside of the 64K DGROUP segment. Technically, this could encompass the entire 1 Megabyte that DOS recognizes, however the memory beyond 640K is reserved for video adapters, the BIOS, expanded memory cards, and the like. BASIC uses far memory (outside the 64K data segment but within the first 640K) for numeric, fixed-length string, and TYPE arrays, although BASIC PDS can optionally store conventional strings there when the /fs (Far String) option is used. Communications buffers are also kept in far memory, and this is where incoming characters are placed before your program actually reads them.
Near memory is therefore very crowded, with many varied types of data competing for space. Earlier I stated that all variables, static arrays, and quoted strings are stored in near memory (DGROUP). But other BASIC data is also stored there as well. This includes DATA items, string descriptors, array descriptors, the stack, file buffers, and the internal working variables used by BASIC's run-time library routines.
When you open a disk file for input, an area in near memory is used as a buffer to improve the speed of subsequent reads. And like subprograms and function that you write, BASIC's internal routines also need their own variables to operate. For example, a translation table is maintained in DGROUP to relate the file numbers you use when opening a file to the file handles that DOS issues.
One final note on the items that compete for DGROUP is that in many cases data is stored *twice*. When you use READ to assign a string from a DATA item, the data itself remains at the data statement, and is also duplicated in the string being assigned. There is simply no way to remove the original data. Similarly, when you assign a string from a constant as in Message$ = "Press any key", the original quoted string is always present, and Message$ receives a second copy. When string space is very tight, the only purely BASIC solution is to instead store the data in a disk file.
Speaking of DATA, bear in mind that reading numeric variables is relatively slow and often even more wasteful. Since all DATA items are stored as strings, each time you use READ the VAL routine is called internally by BASIC. VAL is not a particularly fast operation, because of the complexity of what it must do. Worse, by storing numbers as strings, even more memory can be wasted than you might think. For example, storing an integer value such as -20556 requires six bytes as a string, even though it will be placed ultimately into a two-byte integer.
Since memory is very important to the operation of most programs, it is often useful to know how much of it is available at any given moment. BASIC provides the FRE function to do this, however there are a number of variations in its use. Let's take an inside look at the various forms of FRE, and see how they can be put to good use.
There are no less than six different arguments that can be used with FRE. The first to consider is FRE(0), which reports the amount of free string space but without first compacting the string pool. Therefore, the value returned by FRE(0) may be much lower than what actually could be available. FRE when used with a string argument, for example FRE("") or FRE(Temp$), also returns the amount of DGROUP memory that is available, however it first calls the heap compaction routines. This guarantees that the size reported accurately reflects what is really available.
Although FRE(0) may seem to be of little value, it is in fact much faster than FRE when a string argument is given. Therefore, you could periodically examine FRE(0), and if it becomes unacceptably low use FRE("") to determine the actual amount of memory that is available. With BASIC PDS far strings, FRE(0) is illegal, FRE("") reports the number of bytes available for temporary strings, and FRE(Any$) reports the free size of the segment in which Any$ resides. Temporary strings were discussed earlier, when we saw how they are used when passing fixed-length string arguments to procedures.
FRE(-1) was introduced beginning with QuickBASIC 1, and it reports the total amount of memory that is currently available for use with far arrays. Thus, you could use it in a program before dimensioning a large numeric array, to avoid receiving an "Out of memory" error which would halt your program. Although there is a distinction between near and far memory in any PC program, BASIC does an admirable job of making available as much memory as you need for various uses. For example, it is possible to have plenty of near memory available, but not enough for all of the dynamic arrays that are needed. In this case, BASIC will reduce the amount of memory available in DGROUP, and instead relinquish it for far arrays.
FRE(-1) is also useful if you use SHELL within your programs, because at least 20K or so of memory is needed to load the necessary additional copy of COMMAND.COM. It is interesting to observe that not having enough memory to execute a SHELL results in an "Illegal function call" error, rather than the expected "Out of memory".
FRE(-2) was added to QuickBASIC beginning with version 4.0, and it reports the amount of available stack space. The stack is a special area within DGROUP that is used primarily for passing the addresses of variables and other data to subroutines. The stack is also used to store variables when the STATIC option is omitted from a subprogram or function definition. I will discuss static and non-static subroutines later in Chapter 3, but for now suffice it to say that enough stack memory is necessary when many variables are present and STATIC is omitted.
FRE(-3) was added with BASIC PDS, mainly for use within the QBX editing environment. This newest variant reports the amount of expanded (EMS) memory that is available, although EMS cannot be accessed by your programs directly using BASIC statements. However, QBX uses that memory to store subroutines and optionally numeric, fixed-length, and TYPE arrays. The ISAM file handler that comes with BASIC PDS can also utilize expanded memory, as can the PDS overlay manager.
Besides the various forms of the FRE function, SETMEM can be used to assess the size of the far heap, as well as modify that size if necessary. The STACK function is available only with BASIC PDS, and it reports the largest possible size the stack can be set to. Let's see how these functions can be useful to you.
Although SETMEM is technically a function (because it returns information), it is also used to re-size the far heap. When given an argument of zero, SETMEM returns the current size of the far heap. However, this value is not the amount of memory that is free. Rather, it is the maximum heap size regardless of what currently resides there. The following short program shows this in context.
PRINT SETMEM(0) 'display the heap size REDIM Array!(10000) 'allocate 40,000 bytes PRINT SETMEM(0) 'the total size remains
Displayed result:
276256 276256
When a program starts, the far heap is set as large as possible by BASIC and DOS, which is sensible in most cases. But there are some situations in which you might need to reduce that size, most notably when calling C routines that need to allocate their own memory. Also, BASIC moves arrays around in the far heap as arrays are dimensioned and then erased. This is much like the near heap string compaction that is performed periodically. If the far heap were not rearranged periodically, it is likely that many small portions would be available, but not a single block sufficient for a large array.
In some cases a program may need to claim memory that is guaranteed not to move. Therefore, you could ask SETMEM to relinquish a portion of the far heap, and then call a DOS interrupt to claim that memory for your own use. (DOS provides services to allocate and release memory, which C and assembly language programs use to dimension arrays manually.) Unlike BASIC, DOS does not use sophisticated heap management techniques, therefore the memory it manages does not move. I will discuss using SETMEM this way later on in Chapter 12.
Finally, the STACK function will report the largest amount of memory that can be allocated for use as a stack. Like SETMEM, it doesn't reflect how much of that memory is actually in use. Rather, it simply reports how large the stack could be if you wanted or needed to increase it. Because the stack resides in DGROUP, its maximum possible size is dependent on how many variables and other data items are present.
When run in the QBX environment, the following program fragment shows how creating a dynamic string array reduces the amount of memory that could be used for the stack. Since the string descriptors are kept in DGROUP, they impinge on the potentially available stack space.
PRINT STACK REDIM Array$(1000) PRINT STACK ERASE Array$ PRINT STACK
Displayed result:
47904 43808 47904
Since BASIC PDS does not support FRE(0), the STACK function can be used to determine how much near memory is available. The only real difference between FRE(0) and STACK is that STACK includes the current stack size, where FRE(0) does not. The STACK function is mentioned here because it relates to assessing how much memory is available for data. Sizing the stack will be covered in depth in Chapter 3, when we discuss subprograms, functions, and recursion.
One of the least understood aspects of BASIC programming is undoubtedly the use of VARPTR and its related functions, VARSEG and SADD. Though you probably already know that VARPTR returns the address of a variable, you might be wondering how that information could be useful. After all, the whole point of a high-level language such as BASIC is to shield the programmer from variable addresses, pointers, and other messy low-level details. And by and large, that is correct. Although VARPTR is not a particularly common function, it can be invaluable in some programming situations.
VARPTR is a built-in BASIC function which returns the address of any variable. VARSEG is similar, however it reports the memory segment in which that address is located. SADD is meant for use with conventional (not fixed-length) strings only, and it tells the address where the first character in a string begins. In BASIC PDS, SSEG is used instead of VARSEG for conventional strings, to identify the segment in which the string data is kept. Together, these functions identify the location of any variable in memory.
The primary use for VARPTR in purely BASIC programming is in conjunction with BSAVE and BLOAD, as well as PEEK and POKE. For example, to save an entire array quickly to a disk file with BSAVE, you must specify the address where the array is located. In most cases VARSEG is also needed, to identify the array's segment as well. When used on all simple variables, static arrays, and all string arrays, VARSEG returns the normal DGROUP segment. When used on a dynamic numeric array, it instead returns the segment at the which the specified element resides.
The short example below creates and fills an integer array, and then uses VARSEG and VARPTR to save it very quickly to disk.
REDIM Array%(1 TO 1000) FOR X% = 1 TO 1000 Array%(X%) = X% NEXT DEF SEG = VARSEG(Array%(1)) BSAVE "ARRAY.DAT", VARPTR(Array%(1)), 2000
Here, DEF SEG indicates in which segment the data that BSAVE will be saving is located. VARPTR is then used to specify the address within that segment. The 2000 tells BSAVE how many bytes are to be written to disk, which is determined by multiplying the number of array elements times the size of each element. We will come back to using VARPTR repeatedly in Chapter 11 when we discuss accessing DOS and BIOS services with CALL Interrupt. However, it is important to point out here exactly how VARPTR and VARSEG work with each type of variable.
When VARPTR is used with a numeric variable, as in Address = VARPTR(Value!), the address of the first byte in memory that the variable occupies is reported. Value! is a single-precision variable which spans four bytes of memory, and it is the lowest of the four addresses that is returned. Likewise, VARPTR when used with static fixed-length string and TYPE variables reports the lowest address where the data begins. But when you ask for the VARPTR of a string variable, what is returned is the address of the string's descriptor.
To obtain the address of the actual data in a string requires the SADD (String Address) function. Internally, BASIC simply looks at the address portion of the string descriptor to retrieve the address. Likewise, the LEN function also gets its information directly from the descriptor. When used with any string, VARSEG always reports the normal DGROUP data segment, because that is where all strings and their descriptors are kept.
Beginning with BASIC PDS and its support for far strings, the SSEG function was added to return the segment where the string's data is stored. But even when far strings are being used, VARSEG always returns the segment for the descriptor, which is in DGROUP.
SADD is not legal with a fixed-length string, and you must instead use VARPTR. Perhaps in a future version BASIC will allow either to be used interchangeably. SADD is likewise illegal for use with the fixed-length string portion of a TYPE variable or array. Again, VARPTR will return the address of any component in a TYPE, within the segment reported by VARSEG.
Another important use for VARPTR is to assist passing arrays to assembly language routines. When a single array element is specified using early versions of Microsoft compiled BASIC, the starting address of the element is sent as expected. Beginning with QuickBASIC 4.0 and its support for far data residing in multiple segments, a more complicated arrangement was devised. Here's how that works.
When an element in a dynamic array is passed as a parameter, BASIC makes a copy of the element into a temporary variable in near memory, and then sends the address of the copy. When the routine returns, the data in the temporary variable is copied back to the original array element, in case the called routine changed the data. In many cases this behavior is quite sensible, since the called routine can assume that the variable is in near memory and thus operate that much faster.
Further, BASIC subroutines *require* a non-array parameter (not passed with empty parentheses) to be in DGROUP. That is, any time a single element in an integer array is passed to a routine, that routine would be designed to expect a single integer variable. This is shown in the brief example below, where a single element in an array is passed, as opposed to the entire array.
REDIM Array%(1 TO 100) Array%(25) = -14 CALL MyProc(Array%(25)) 'pass one element . . . SUB MyProc(IntVar%) STATIC 'this sub expects a PRINT IntVar% ' single variable END SUB
Displayed result:
-14
Unfortunately, this copying not only generates a lot of extra code to implement, it also takes memory from DGROUP to hold the copy, and that memory is taken permanently. Worse still, *each* occurrence of an array element passed in a CALL statement reserves however many bytes are needed to store the element. For a large TYPE structure this can be a lot of memory indeed!
So you won't think that I'm being an alarmist about this issue, here are some facts based on programs compiled using BASIC 7.1 PDS. These examples document the amount of additional code that is generated to pass a near string array element as an argument to a subprogram or function.
Passing a string array element requires 56 bytes when a copy is made, compared to only 17 when it is not. The same operations in QuickBASIC 4.5 create 47 and 18 bytes respectively, so QB 4.5 is actually better when making the copy, but a tad worse when not. The code used in these examples is shown below, and Array$ is a dynamic near string array. (I will explain the purpose of BYVAL in just a moment.) Again, the difference in byte counts reflects the additional code that BC creates to assign and then delete the temporary copies.
CALL Routine(Array$(2)) CALL Routine(BYVAL VARPTR(Array$(2)))
Worse still, with either compiler 73 bytes of code are created to pass an element in a TYPE array the usual way, compared to 18 when the copying is avoided. And this byte count does not include the DGROUP memory required to hold the copy. Is that reduction in code size worth working for? You bet it is! And best of all, hardly any extra effort is needed to avoid having BASIC make these copies--just the appropriate knowledge.
The key, as you can see, is VARPTR. If you are calling an assembly language routine that expects a string and you want to pass an element from a string array, you must use BYVAL along with VARPTR. CALL Routine(BYVAL VARPTR(Array$(Element))) is functionally identical to CALL Routine(Array$(Element)), although they sure do look different! In either case, the integer address of a string is passed to the routine.
Unlike the usual way that BASIC passes a variable by sending its address, BYVAL instead sends the actual data. In this case, the value of an address is what we wanted to begin with anyway. (Without the BYVAL, BASIC would make a temporary copy of the integer value that VARPTR returns, and send the address of that copy.) Best of all, asking for the address directly defeats the built-in copying mechanism. Although creating a copy of a far numeric array element is sensible as we saw earlier, it is not clear to me why BC does this with string array data that is in DGROUP already.
Although you can't normally send an integer--which is what VARPTR actually returns--to a BASIC subprogram that expects a string, you can if that subprogram is in a different file and the files are compiled separately. This will also work if the BASIC code has been pre-compiled and placed in a Quick Library.
But there is another, equally important reason to use VARPTR with array elements. If you are calling an assembler routine that will sort an array, it must have access to the array element's address, and not the address of a copy. All of the elements in any array are contiguous, and a sort routine would need to know where in memory the first element is located. From that it can then access all of the successive elements. With VARPTR we are telling BASIC that what is needed is the actual address of the specified element.
Bear in mind that this relates primarily to passing arrays to assembly language (and possibly C) routines only. After all, if you are designing a sort routine using purely BASIC commands, you would pass and receive the array using empty parentheses. Indeed, this is yet another important advantage that BASIC holds over C and Pascal, since neither of those languages have array descriptors. Writing a sort routine in C requires that *you* do all of the work to locate and compare each element in turn, based on some base starting address.
There is one final issue that we must discuss, and that is passing far array data to external assembly language routines. I already explained that by making a copy of a far array element, the called routine does not have to be written to deal with far (two-word segmented) addresses. But in some cases, writing a routine that way will be more efficient. Further, like C, assembly language routines thrive on manipulating pointers to data. Although an assembler routine could be written to read the segment and address from the array descriptor, this is not a common method. One reason is that if Microsoft changes the format of the descriptor, the routine will no longer work. Another is that it is frankly easier to have the caller simply pass the full segmented address of the first element.
This brings us to the SEG directive, which is a combination of BYVAL and VARPTR and also BYVAL and VARSEG. As with BYVAL VARPTR, using SEG before a variable or array element in a call tells BASIC that the value of the array's full address is needed. A typical example would be CALL Routine(SEG Array#(1)), and in this case, BASIC sends not one address word but two to the routine.
You could also pass the full address of an array element by value using VARSEG and VARPTR, and this next example produces the identical result: CALL Routine(BYVAL VARSEG(Array#(1)), BYVAL VARPTR(Array#(1))). Using SEG results in somewhat less code, though, because BASIC will obtain the segment and address in a single operation. In fact, this is one area where the compiler does a poor job of optimizing, because using VARSEG and VARPTR in a single program statement generates a similar sequence of code twice.
There is one unfortunate complication here, which arises when SEG is used with a fixed-length string array. What SEG *should* do in that case is pass the segmented address of the specified element. But it doesn't. Instead, BASIC creates a temporary copy of the specified element in a conventional dynamic string, and then passes the segmented address of the copy's descriptor. Of course, this is useless in most programming situations.
There are two possible solutions to this problem. The first is to use the slightly less efficient BYVAL VARSEG and BYVAL VARPTR combination as shown above. The second solution is to create an equivalent fixed-length string array by using a dummy TYPE that is comprised solely of a single string component. Since TYPE variables are passed correctly when SEG is used, using a TYPE eliminates the problem. Both of these methods are shown in the listing that follows.
'----- this creates more code and looks clumsy REDIM Array(1 TO 1000) AS STRING * 50 CALL Routine(BYVAL VARSEG(Array(1)), BYVAL VARPTR(Array(1))) '----- this creates less code and reads clearly TYPE FLen S AS STRING * 100 END TYPE REDIM Array(1 TO 1000) AS FLen CALL Routine(SEG Array(1))
Although SEG looks like a single parameter is being passed, in fact two integers are sent to the called routine--a segment and an address. This is why a single SEG can replace both a VARSEG and a VARPTR in one call. Chapter 12 will return to BYVAL, VARPTR, and SEG, though the purpose there will be to learn how to write routines that accept such parameters.
The final data type to examine is constants. By definition, a constant is simply any value that does not change, as opposed to a variable that can. For example, in the statement I% = 10, the value 10 is a constant. Similarly, the quoted string "Hello" is a constant when you write PRINT "Hello".
There are two types of constants that can appear in a BASIC program. One is simple numbers and quoted strings as described above, and the other is the named constant which is defined using a CONST statement. For example, you can write CONST MaxRows = 25 as well as CONST Message$ = "Insert disk in drive", and so forth. It is even possible to define one CONST value based on a previous one, as in CONST NumRows = 25, ScrnSize = NumRows * 80. Then, you could use these meaningful names later in the program, instead of the values they represent.
It is important to understand that using named constants is identical to using the numbers themselves. The value of this will become apparent when you see the relative advantages and disadvantages of using numbers as opposed to variables. Let's begin this discussion of numbers with how they are stored by the compiler. Or rather, how they are sometimes stored.
When a CONST statement is used in a BASIC program, BASIC does absolutely nothing with the value, other than to remember that you defined it. Therefore, you could have a hundred CONST statements which are never used, and the final .EXE program will be no larger than if none had been defined. If a CONST value is used as an argument to, say, LOCATE or perhaps as a parameter to a subroutine, BASIC simply substitutes the value you originally gave it. When a variable is assigned as in Value% = 100, BASIC sets aside memory to hold the variable. With a constant definition such as CONST Value% = 100, no memory is set aside and BASIC merely remembers that any use of Value% is to be replaced by the number 100. But how are these numbers represented internally.
When you create an integer assignment such as Count% = 5, the BASIC compiler generates code to move the value 5 into the integer variable, as you saw in Chapter 1. Therefore, the actual value 5 is never stored as data anywhere. Rather, it is placed into the code as part of an assembly language instruction.
Now, if you instead assign a single or double precision variable from a number--and again it doesn't matter whether that number is a literal or a CONST--the appropriate floating point representation of that number is placed in DGROUP at compile time, and then used as the source for a normal floating point assignment. That is, it is assigned as if it were a variable.
There is no reasonable way to imbed a floating point value into an assembly language instruction, because the CPU cannot deal with such values directly. Therefore, assigning X% = 3 treats the number 3 as an integer value, while assigning Y# = 3 treats it as a double precision value. Again, it doesn't matter whether the 3 is a literal number as shown here, or a CONST that has been defined. In fact, if you use CONST Three! = 3, a subsequent assignment such as Value% = Three! treats Three! as an integer resulting in less resultant code. As you can see, the compiler is extremely smart in how it handles these constants, and it understands the context in which they are being used.
In general, BASIC uses the minimum precision possible when representing a number. However, you can coerce a number to a different precision with an explicit type identifier. For example, if you are calling a routine in a separate module that expects a double precision value, you could add a pound sign (#) to the number like this: CALL Something(45#). Without the double precision identifier, BASIC would treat the 45 as an integer, which is of course incorrect.
Likewise, BASIC can be forced to evaluate a numeric expression that might otherwise overflow by placing a type identifier after it. One typical situation is when constructing a value from two byte portions. The usual way to do this would be Value& = LoByte% + 256 * HiByte%. Although the result of this expression can clearly fit into the long integer no matter what the values of LoByte% and HiByte% might be, an overflow error can still occur. (But as we saw earlier, this will happen only in the QB environment, or if you have compiled to disk with the /d debugging option.)
The problem arises when HiByte% is greater than 127, because the result of multiplying HiByte% times 256 exceeds the capacity of a regular integer. Normally, BASIC is to be commended for the way it minimizes overhead by reducing calculations to the smallest possible data type. But in this case it creates a problem, because the result cannot be expressed as an integer.
The solution, then, is to add an ampersand after the 256, as in Value& = LoByte% + 256& * HiByte%. By establishing the value 256 as a long integer, you are telling BASIC to perform the calculation to the full precision of a long integer. And since the result of the multiplication is treated as a long integer, so is the addition of that result to LoByte%. A single precision exclamation point could also be used, but that would require a floating point multiplication. Since a long integer multiply is much faster and needs less code, this is the preferred solution.
One final item worth noting is the way the QB and QBX editing environments sometimes modify constants. For example, if you attempt to enter a statement such as Value! = 1.0, you will see the constant changed to read 1! instead. This happens when you press Enter to terminate the line. Similarly, if you write D# = 1234567.8901234, BASIC will add a trailing pound sign to the number. This behavior is your clue that these numbers are being stored internally as single and double precision values respectively.
Normally, any constant that could be an integer is passed to a subprogram or function as an integer. That is, calling an external procedure as in CALL External(100) passes the 100 as an integer value. If the called routine has been designed to expect a variable of a different type, you must add the appropriate type identifier. If a long integer is expected, for example, you must use CALL External(100&). If, on the other hand, the called routine is in the same module (that is, the same physical source file), QB will create a suitable DECLARE statement automatically. This lets QB and BC know what is expected so they can pass the value in the correct format. Thus, BASIC is doing you a favor by interpreting the constant's type in a manner that is relevant to your program.
This "favor" has a nasty quirk, though. If you are developing a multi-module program in the QuickBASIC editor, the automatic type conversion is done for you automatically, even when the call is to a different module. Your program uses, say, CALL Routine(25), and QB or QBX send the value in the correct format automatically. But when the modules are compiled and linked, the same program that had worked correctly in the environment will now fail.
Since each module in a multi-module program is compiled separately, BC has no way to know what the called routine actually expects. In fact, this is one of the primary purposes of the DECLARE statement--to advise BASIC as to how arguments are to be passed. For example, DECLARE SUB Marine(Trident!) tells BASIC that any constant passed to Marine is to be sent as a single precision value. You could optionally use the AS SINGLE directive, thus: DECLARE SUB Marine(Trident AS SINGLE). In general, I prefer the more compact form since it conveys the necessary information with less clutter.
Another important use for adding a type identifier to a numeric constant is to improve a program's accuracy. Running the short program below will illustrate this in context. Although neither answer is entirely accurate, the calculation that uses the double precision constant is much closer. In this case, a decimal number that does not have an explicit type identifier is assumed to have only single precision accuracy. That is, the value is stored in only four bytes instead of eight.
FOR X% = 1 TO 10000 Y# = Y# + 1.1 Z# = Z# + 1.1# NEXT PRINT Y#, Z#
Displayed result:
11000.00023841858 11000.00000000204
You have already learned that BASIC often makes a temporary copy of a variable when calling a subprogram or function. But you should know that this also happens whenever a constant is passed as an argument. For example, in a function call such as Result = Calculate!(Value!, 100), where Calculate! has been declared as a function, the integer value 100 is copied to a temporary location. Since BASIC procedures require the address of a parameter, a temporary variable must be created and the address of that variable passed. The important point to remember is that for each occurrence of a constant in a CALL or function invocation, a new area of DGROUP is taken.
You might think that BASIC should simply store a 100 somewhere in DGROUP once, and then pass the address of that value. Indeed, this would save an awful lot of memory when many constants are being used. The reason this isn't done, however, is that subroutines can change incoming parameters. Therefore, if a single integer 100 was stored and its address passed to a routine that changed it, subsequent calls using 100 would receive an incorrect value.
The ideal solution to this problem is to create a variable with the required value. For example, if you are now passing the value 2 as a literal many times in a program, instead assign a variable, perhaps named Two%, early in your program. That is, Two% = 2. Then, each time you need that value, instead pass the variable. For the record, six bytes are needed to assign an integer such as Two%, and four bytes are generated each time that variable is passed in a call.
Contrast that to the 10 bytes generated to create and store a temporary copy and pass its address, not including the two bytes the copy permanently takes from near memory. Even if you use the value only twice, the savings will be worthwhile (24 vs. 30 bytes). Because a value of zero is very common, it is also an ideal candidate for being replaced with a variable. Even better, you don't even have to assign it! That is, CALL SomeProc(Zero%) will send a zero, without requiring a previous Zero% = 0 assignment.
Like numeric constants, string constants that are defined in a CONST statement but never referenced will not be added to the final .EXE file. Constants that are used--whether as literals or as CONST statements--are always stored in DGROUP. If your program has the statement PRINT "I like BASIC", then the twelve characters in the string are placed into DGROUP. But since the PRINT statement requires a string descriptor in order to locate the string and determine its length, an additional four bytes are allocated by BASIC just for that purpose. Variables are always stored at an even-numbered address, so odd-length strings also waste one extra byte.
Because string constants have a ferocious appetite for near memory, BC has been designed to be particularly intelligent in the way they are handled. Although there is no way to avoid the storage of a descriptor for each constant, there is another, even better trick that can be employed. For each string constant you reference in a program that is longer than four characters, BC stores it only once. Even if you have the statement PRINT "Press any key to continue" twenty-five times in your program, BC will store the characters just once, and each PRINT statement will refer to the same string.
In order to do this, the compiler must remember each string constant it encounters as it processes your program, and save it in an internal working array. When many string constants are being used, this can cause the compiler to run out of memory. Remember, BC has an enormous amount of information it must deal with as it processes your BASIC source file, and keeping track of string constants is but one part of the job.
To solve this problem Microsoft has provided the /s (String) option, which tells BC not to combine like data. Although this may have the net effect of making the final .EXE file larger and also taking more string space, it may be the only solution with some large programs. Contrary to the BASIC documentation, however, using /s in reality often makes a program *smaller*. This issue will be described in detail in Chapter 5, where all of the various BC command line options are discussed.
As you have repeatedly seen, BASIC often generates additional code to create copies of variables and constants. It should come as no surprise, therefore, to learn that this happens with string constants as well. When you print the same string more than once in a program, BASIC knows that its own PRINT routine will never change the data. But as with numeric constants, if you send a string constant to a subprogram or function, there is no such guarantee.
For example, if you have a statement such as CALL PrintIt(Work$) in your program, it is very possible--even likely--that the PrintIt routine may change or reassign its incoming parameter. Even if *you* know that PrintIt will not change the string, BASIC has no way to know this. To avoid any possibility of that happening, BASIC generates code to create a temporary copy of every string constant that is used as an argument. And this is done for every call. If the statement CALL PrintMessage("Press a key") appears in your program ten times, then code to copy that message is generated ten times!
Beginning with BASIC 7.1 PDS, you can now specify that variables are to be sent by value to BASIC procedures. This lets you avoid the creation of temporary copies, and this subject will also be explored in more detail in Chapter 3.
With either QuickBASIC 4.5 or BASIC PDS, calling a routine with a single quoted string as an argument generates 31 bytes of code. Passing a string variable instead requires only nine bytes. Both of these byte counts includes the five bytes to process the call itself. The real difference is therefore 4 bytes vs. 26--for a net ratio of 6.5 to 1. (Part of those 31 bytes is code that erases the temporary string.) So as with numeric constants that are used more than once, your programs will be smaller if a variable is assigned once, and that variable is passed as an argument.
While we are on the topic of temporary variables, there is yet another situation that causes BASIC to create them. When the result of an expression is passed as an argument, BASIC must evaluate that expression, and store the result somewhere. Again, since nearly all procedures require the address of a parameter rather than its value, an address of that result is needed. And without storing the result, there can of course be no address.
When you use a statement such as CALL Home(Elli + Lou), BASIC calculates the sum of Elli plus Lou, and stores that in a reserved place in DGROUP which is not used for any other purpose. That address is then sent to the Home routine as if it were a single variable, and Home is none the wiser. Likewise, a string concatenation creates a temporary string, for the same reason. Although the requisite descriptor permanently steals four bytes of DGROUP memory, the temporary string itself is erased by BASIC automatically after the call. Thus, the first example in the listing below is similar in efficiency to the second. The four-byte difference is due to BASIC calling a special routine that deletes the temporary copy it created, as opposed to the slightly more involved code that assigns Temp$ from the null string ("") to erase it.
CALL DoIt(First$ + Last$) 'this makes 41 bytes Temp$ = First$ + Last$ 'this makes 45 bytes CALL DoIt(Temp$) Temp$ = ""
One final topic worth mentioning is that QuickBASIC also lets you imbed control and extended characters into a string constant. Consider the program shown below. Here, several of the IBM extended characters are used to define a box, but without requiring CHR$ to be used repeatedly. Characters with ASCII values greater than 127 can be entered easily by simply pressing and holding the Alt key, typing the desired ASCII value on the PC's numeric key-pad, and then releasing the Alt key. This will not work using the number keys along the top row of the keyboard.
DIM Box$(1 TO 4) 'define a box Box$(1) = "ΙΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝ»" Box$(2) = "Ί Ί" Box$(3) = "Ί Ί" Box$(4) = "ΘΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝΝΌ" FOR X = 1 TO 4 'now display the box PRINT Box$(X) NEXT
To enter control characters (those with ASCII values less than 32) requires a different trick. Although the Alt-keypad method is in fact built into the BIOS of all PCs, this next one is specific to QuickBASIC, QBX, and some word processor programs. To do this, first press Ctrl-P, observing the ^P symbol that QB displays at the bottom right of the screen. This lets you know that the next control character you press will be accepted literally. For example, Ctrl-P followed by Ctrl-L will display the female symbol, and Ctrl-P followed by Ctrl-[ will enter the Escape character.
Bear in mind that some control codes will cause unusual behavior if your program is listed on a printer. For example, an embedded CHR$(7) will sound the buzzer if your printer has one, a CHR$(8) will back up the print head one column, and a CHR$(12) will issue a form feed and skip to the next page. Indeed, you can use this to advantage to intentionally force a form feed, perhaps with a statement such as REM followed by the Ctrl-L female symbol.
I should mention that different versions of the QB editor respond differently to the Ctrl-P command. QuickBASIC 4.0 requires Ctrl-[ to enter the Escape code, while QBX takes either Ctrl-[ or the Escape key itself. I should also mention that you must never imbed a CHR$(26) into a BASIC source file. That character is recognized by DOS to indicate the end of a file, and BC will stop dead at that point when compiling your program. QB, however, will load the file correctly.
No discussion of constants would be complete without a mention of initialized data. Unfortunately, as of this writing BASIC does not support that feature! The concept is simple, and it would be trivial for BASIC's designers to implement. Here's how initialized data works.
Whenever a variable requires a certain value, the only way to give it that value is to assign it. Some languages let you declare a variable's initial value in the source code, saving the few bytes it takes to assign it later. Since space for every variable is in the .EXE file anyway, there would be no additional penalty imposed by adding this capability. I envision a syntax such as DIM X = 3.9 AS SINGLE, or perhaps simply DIM Y% = 3, or even DIM PassWord$ = "GuessThis". Where Y% = 3 creates a six-byte code sequence to put the value 3 into Y%, what I am proposing would have the compiler place that value there at the time it creates the program.
Equally desireable would be allowing string constants to be defined using CHR$ arguments. For example, CONST EOF$ = CHR$(26) would be a terrific enhancement to the language, and allowing code such as CONST CRLF$ = CHR$(13) + CHR$(10) would be even more powerful. Again, we can only hope that this feature will be added in a future version.
Yet another constant optimization that BASIC could do but doesn't is constant string function evaluation. In many programming situations the programmer is faced with deciding between program efficiency and readability. A perfect example of this is testing an integer value to see whether it represents a legal character. For instance, IF Char < 65 is not nearly as meaningful as IF Char < ASC("A").
Clearly, BC could and should resolve the expression ASC("A") while it is compiling your program, and generate simple code that compares two integers. Instead, it stores the "A" as a one-byte string (which with its descriptor takes five bytes), and generates code to call the internal ASC function before performing the comparison. The point here is that no matter how intelligent BC is, folks like us will always find some reason to complain!
The last important subject this chapter will cover is bit manipulation using AND, OR, XOR, and NOT. These logical operators have two similar, but very different, uses in a BASIC program. The first use--the one I will discuss here--is to manipulate the individual bits in an integer or long integer variable. The second use is for directing a program's flow, and that will be covered in Chapter 3.
Each of the bit manipulation operators performs a very simple Binary function. Most of these functions operate on the contents of two integers, using those bits that are in an equivalent position. The examples shown in Figure 2-6 use a single byte only, solely for clarity. In practice, the same operations would be extended to either the sixteen bits in an integer, or the 32 bits in a long integer.
13 = 0000 1101
25 = 0001 1001
=========
0000 1001 result when AND is used
^ ^
+--+-------- both of the bits are set
in each column
13 = 0000 1101
25 = 0001 1001
=========
0001 1101 result when OR is used
^ ^^ ^
+-++-+-------- one or both bits are set
in each column
13 = 0000 1101
25 = 0001 1001
=========
0001 0100 result when XOR is used
^ ^
+--+---------- the bits are different
in each column
13 = 0000 0000 0000 1101
===================
1111 1111 1111 0010 result after using NOT
The examples given here use the same decimal values 13 and 25, and these are also shown in their Binary equivalents. What is important when viewing Binary numbers is to consider the two bits in each vertical column. In the first example, the result in a given column is 1 (or True) only when that bit is set in the first number AND the same bit is also set in the second. This condition is true for only two of the bits in these particular numbers. The result bits therefore represent the answer in Binary, which in this case is 13 AND 25 = 9. What is important here is not that 13 AND 25 equals 9, but how the bits interact with each other.
The second example shows OR at work, and it sets the result bits for any position where a given bit is set in one byte OR that bit is set in the other. Of course, if both are set the OR result is also true. In this case, four of the columns have one bit or the other (or both) set to 1. By the way, these results can be proven easily in BASIC by simply typing the expression. That is, PRINT 13 OR 25 will display the answer 29.
The third example is for XOR, which stands for Exclusive Or. XOR sets a result bit only when the two bits being compared are different. Here, two of the bits are different, thus 13 XOR 25 = 20. Again, it is not the decimal result we are after, but how the bits in one variable can be used to set or clear the bits in another.
The NOT operator uses only one value, and it simply reverses all of the bits. Any bit that was a 1 is changed to 0, and any bit that had been 0 is now 1. A full word is used in this example, to illustrate the fact that NOT on any positive number makes it negative, and vice versa. As you learned earlier in this chapter, the highest, or left-most bit is used to store the sign of a number. Therefore, toggling this bit also switches the number between positive and negative. In this case, NOT 13 = -14.
All of the logical operators can be very useful in some situations, although admittedly those situations are generally when accessing DOS or interfacing with assembly language routines. For example, many DOS services indicate a failure such as "File not found" by setting the Carry flag. You would thus use AND after a CALL Interrupt to test that bit. Another good application for bit manipulation is to store True or False information in each of the sixteen bits in an integer, thus preserving memory. That is, instead of sixteen separate Yes/No variables, you could use just one integer.
Bit operations can also be used to replace calculations in certain situations. One common practice is to use division and MOD to break an integer word into its component byte portions. The usual way to obtain the lower byte is LoByte% = Word% MOD 256, where MOD provides the remainder after dividing. While there is nothing wrong with doing it that way, Word% = LoByte% AND 255 operates slightly faster. Division is simply a slower operation than AND, especially on the 8088. Newer chips such as the 80286 and 80386 have improved algorithms, and division is not nearly as slow as with the older CPU. Chapter 3 will look at some other purely BASIC uses of AND and OR.
As you have seen in this chapter, there is much more to variables and data than the BASIC manuals indicate. You have learned how data is constructed and stored, how the compiler manipulates that data, and how to determine for yourself the amount of memory that is needed and is available. In particular, you have seen how data is copied frequently but with no indication that this is happening. Because such copying requires additional memory, it is a frequent cause of "Out of memory" errors that on the surface appear to be unfounded.
You have also learned about BASIC's near and far heaps, and how they are managed using string and array descriptors. With its dynamic allocation methods and periodic rearrangement of the data in your program, BASIC is able to prevent memory from becoming fragmented. Although such sophisticated memory management techniques require additional code to implement, they provide an important service that programmers would otherwise have to devise for themselves.
Finally, you have learned how the various bit manipulation operations in BASIC work. This chapter will prove to be an important foundation for the information presented in upcoming chapters. Indeed, a thorough understanding of data and memory issues will be invaluable when you learn about accessing DOS and BIOS services in Chapter 11.