Polar plasmas
I am really wondering how many diferrent types of plasma effects do there exist. Sometimes, when I code a new 2d effect, some friends from the scene tell me "Wow! Nice plasma!!!" (Especially the ones who aren't much into modern effects or graphics coding in general). I try then to explain them that it's something more than a plasma, a new effect I've just coded that takes again the concept of painting each pixel by a color that depends on a function using the pixel coordinates. Would that be considered as a plasma effect? Dunno. And yet there are still several 2d pixel effects whose I neither know their real names nor I have tried to code them. Some of them are just variations or combinations of what I've coded before. Those effects my friends still tend to call plasmas are maybe in this category. One of my favorites are those whirlwinds or flowers that I would call polar plasmas here.
The concept is quite easy. In regular plasmas the color of each pixel came from a function that added the sines of x and y of the current pixel plus even more combinations of random sines of x and y. Now, if each pixel can be represented with two variables, the angle and distance from the center of the screen, then we just take the color as a function of these two variables for each pixel and have beautiful circular color shapes instead!
I will try to explain myself soon..
First of all, we have to get the radius and angle of each pixel from the center of the screen (That is near to (160,120) if we are working in 320x240 resolution). We wouldn't like to do this in realtime because we need to use SQR for the radius and ATAN2 for the angle. So, all that is needed is to precalculate two big arrays of size 320*240 each. This is how we do it:
const SCR_WIDTH = 320
const SCR_HEIGHT = 240
const SCR_SIZE = SCR_WIDTH * SCR_HEIGHT
const xc% = SCR_WIDTH / 2
const yc% = SCR_HEIGHT / 2
const rang% = 512
const pi = 3.14151693
const d2r = 180/pi
const d2b = (rang% * d2r) / 360
dim shared radius(SCR_SIZE-1) as ubyte, angle(SCR_SIZE-1) as ubyte
i% = 0
for y% = 0 to SCR_HEIGHT - 1
for x% = 0 to SCR_WIDTH - 1
xs% = x% - xc%
ys% = y% - yc%
radius(i%) = sqr(xs% ^ 2 + ys% ^ 2)
angle(i%) = atan2(xs%, ys%) * d2b
i% = i% + 1
next x%
next y%
xc% and yc% are the x and y coordinates of the pixel on the center of the screen. We have two tables, radius and angle, holding the radius and angle of each pixel on the screen. These two tables could be two dimensional to make things more clear but I just copied the code from my old sources, it's faster this way anyways. Just imagine that the upper-left pixel onto the screen is the very 1st element of our array and as we move to the next byte, we also move to the next pixel in the right, exactly the same way you talk to your videobuffer. Anyways, I think most of you have no problem with that so I don't need to explain. These tables corresponds with the same pixels in your videobuffer.
As you may know, to get the distance of (x1,y1) from (x0,y0) you just need to calculate SQR((x1-x0)^2 + (y1-y0)^2). That's math. Here, (x0,y0) could be the center of the screen and (x1,y1) variable for each diferrent pixel. We calculate those diferrences in xs% and ys% and the distance is given by SQR(xs%^2 + ys%^2). Preety simple! As for the angle, ATAN2 is a quite useful function that returns the angle in rads between the line from a point to (0,0) and the X axis. Simply, it returns the angle of a given point based on it's x and y coordinates. Actually atn is the inverse function of tangent but atan2 is a better version of it. In the past I used atn but I had to split the code in 4 cases according to the quarter my pixel was, for some mathematical reasons I can't explain here this didn't worked easilly. But thanks to rel who pointed it out to me, atan2 does the job alone!
And there is a reason we multiply the result by d2b. Above in the consts, we've made some hocus pocus, nothing else than calculating some consts useful for converting from radians to degrees and the opposite. By multiplying by d2r you convert radians to degrees and by dividing by d2r the opposite happens. That's because we know from math that one rad equals 180/pi degrees. But why calculating d2b based on a const named rang% and using this one instead? I just want to be sure that the angle values cycle from 0 to 512 instead from 0 to 360 and that's because I am later using a table of 256 colors pallete with continuous colors that cycle after 255 from 0. Else, you will see a harsh bug in your polar plasmas, except if you also use a 360 color pallete that cycles it's colors at the end :)
Here is an example of the little code that generates some palete in 32bit mode. When I say the color cycles after 255, I mean that if the color fades to black till 255 it should start from black at 0. In our polar plasma, color addition might give overflows (values over 255 that start from 0, if we use unsigned byte for our color variable) but if we make the shade table appropriately, we have smooth color and no clashes. Maybe you are still wondering why I didn't put rang%=256 but 512, but there is no problem with that, cause the angle ends well enough at 511 which is 255 in ubyte. If you put multiplies of 256 in rang% you see your shapes change. But don't worry about that for the moment..
dim shared pal%(255)
for i%=0 to 63
pal%(i%)=(i%*2) shl 16 or i%*4
pal%(i%+64)=(128+i%*2) shl 16 or (i%*4) shl 8 or (63-i%)*4
pal%(i%+128)=255 shl 16 or ((63-i%)*4) shl 8
pal%(i%+192)=((63-i%)*4) shl 16
next i%

And now to the point:
Before we start though, we'll precalculate some sines we will need later..
l!=0.25
for i%=0 to 2047
fsin1%(i)=sin(i%/(l!*d2b))*48+64
fsin2%(i)=sin(i%/(l!*d2b/2))*40+48
next i%
And now we are ready..
Which shape would we get if each pixel was colored after it's radius from the center?
dim c as ubyte
for i%=0 to SCR_SIZE-1
c= radius(i%)
vram(i%) = pal(c)
next i%

And what would happen if each pixel was colored after it's angle?
dim c as ubyte
for i%=0 to SCR_SIZE-1
c= angle(i%)
vram(i%) = pal(c)
next i%

Now imagine adding these two!
dim c as ubyte
for i%=0 to SCR_SIZE-1
c= radius(i%) + angle(i%)
vram(i%) = pal(c)
next i%
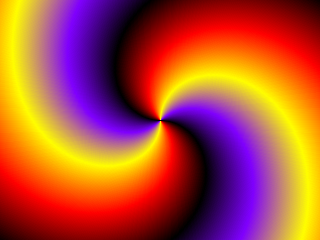
Now about the next shape. I hope that till know you can easilly imagine the corresponding of the images with the actual code. How about a flower shape now?
Just imagine taking the first case with the colored cycles, but now trying to manipulate it's code so that the radial color is disturbed in diferrent angles. That's how the flower shape looks like! At diferrent angles the colors are more open, you say the same color in further distance in one angle from the other. Just imagine taking the first case with the colored circles, where at the same radius the color is the same. And disturbing that fact by adding a sine function of the radius! We use the precalculated sines to make the disturbance being wavy! And of course the sines were also generated by using d2b so that there are no bugs with color overflows.
dim c as ubyte
for i%=0 to SCR_SIZE-1
c = radius(i%) + fsin2%(angle(i%))
vram(i%) = pal(c)
next i%

And here in short, we have some nice examples of shapes that can be produced by these codes:
dim c as ubyte
for i%=0 to SCR_SIZE-1
c = radius(i%) + fsin2%(radius(i%) + angle(i%))
vram(i%) = pal(c)
next i%

But till now we only had static plasmas! Of course, but if you put a variable (k% here) inside some of the sines, which you increase per each frame (either by addition or preferably by the timer) you have some great moving shit!!!
dim c as ubyte
for i%=0 to SCR_SIZE-1
c = angle(i%) + fsin1%(radius(i%) + fsin2%(radius(i%) + k%))
vram(i%) = pal(c)
next i%
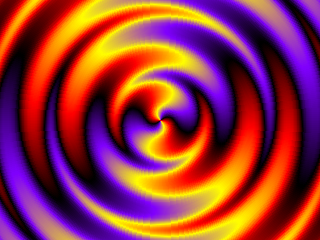
You can experiment and make much more cooler shapes! I am still amazed by what was produced and I still fiddled with my code during the writting of this tutorial to discover more wild stuff! I hope I explained the whole stuff well here, though I wrote this tutorial really fast to support the magazine. I never expected it will all end up like this in such a hurried article. Still, if you have any questions or problems with these codes, feel free to send me an email at optimus6128@yahoo.gr. See you in my next tutorial (if there will be any soon) ;P
Michael Kargas aka Optimus






